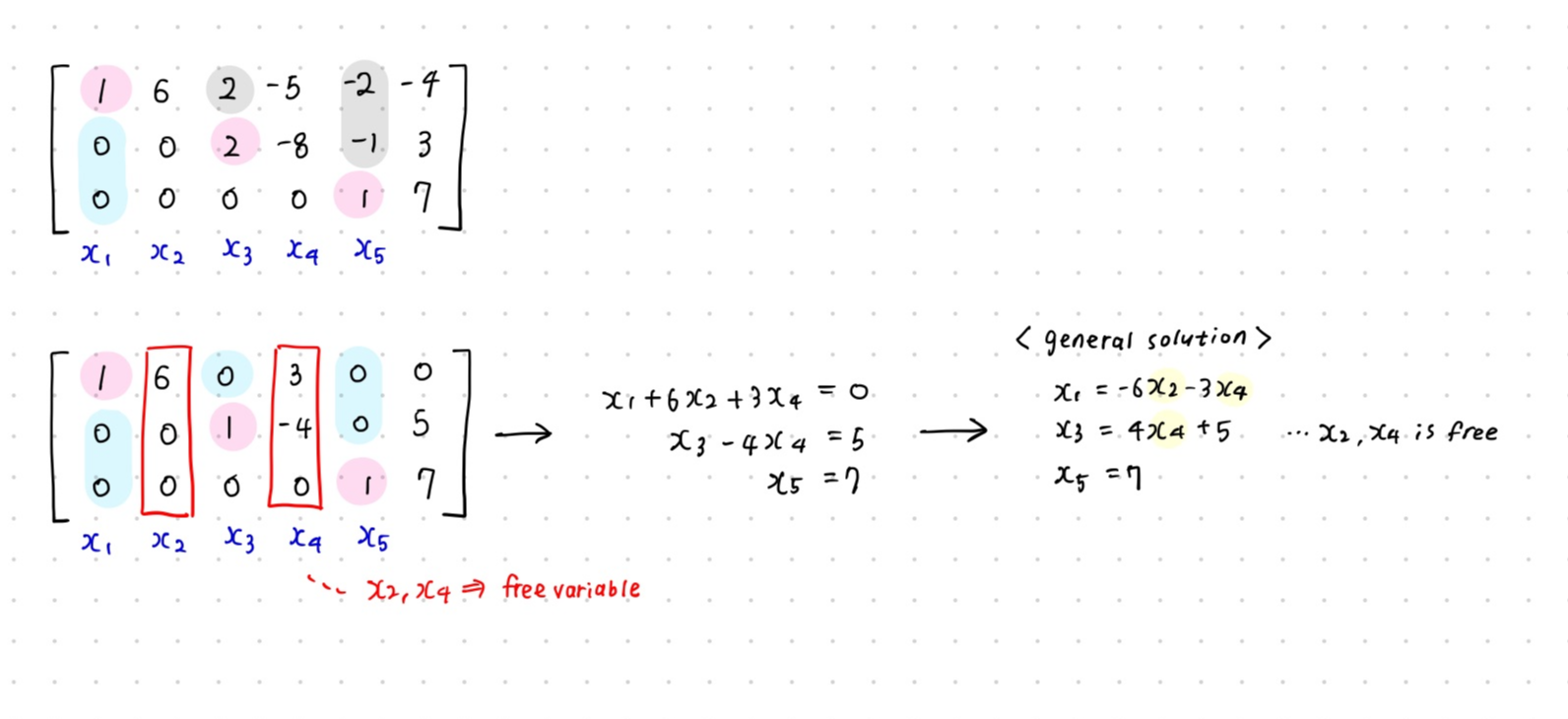
- basic variable : corresponds to a pivot column (pivot column에 있는 변수)
- free variable : columns that don't have a leading variable. (pivot 포지션이 없는 column에 있는 변수)
- general solution : 'Ax = b' 형태, free variable을 이용하여 표현한다.
- Existence and Uniqueness Theorem
: A linear system is consistent if and only if the rightmost column of the augmented matrix is not a pivot column.
That is, if and only if an echelon form of the matrix does not have a row of the form: [0 0 ··· 0 b], with b != 0.
: 해가 consistent 하고 단일인 경우, augmented matrix의 가장 오른쪽 column은 pivot column이 아니어야한다.
(pivot column에는 반드시 0이 포함되고, 0 = b 이면 해가 단일일 수 없기 때문)
즉, echelon form의 row에 [0 0 ··· 0 b] 이러한 형태가 없어야 한다. (b가 nonzero일 때)
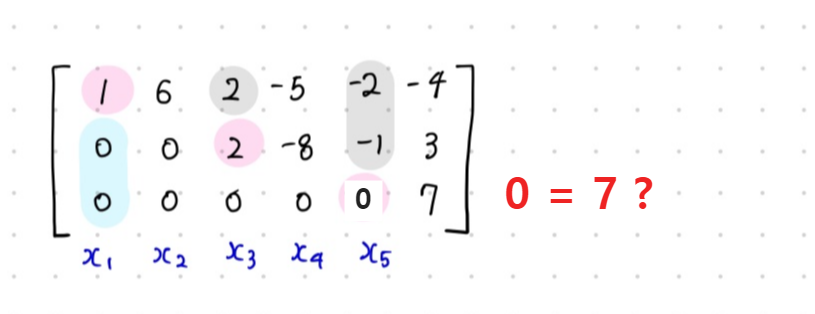
: linear system 이 consistent 하고 단일 solution 을 가진 경우, solution set에 free variable이 없어야한다.
: 무한한 solution을 가진 경우, solution set에 free variable이 최소 1개 이상 있어야한다.
'통계 > 선형대수 (Linear Algebra)' 카테고리의 다른 글
| Linear Independence (0) | 2024.06.09 |
|---|---|
| Homogeneous system (0) | 2024.06.08 |
| Vector equations & Scalar (0) | 2024.06.08 |
| Echelon Forms (0) | 2024.06.08 |
| System of Linear Equations (0) | 2024.06.07 |
